
|




Nurikabe Strategy Tips
Nurikabe is a very playable puzzle, and you need surprisingly few numbers to placed in the grid to allow you to solve a puzzle - as long as you use the right tactics to help you solve the puzzle!
Here are a few strategy tips for nurikabe:
1) Fill in squares between separate islands
This is one of the simplest things to do but an important part of the strategy whilst solving a puzzle. It is in accordance with the rules that islands cannot touch.
So, look at this section of a puzzle:
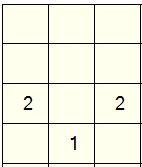
We know that the two '2's must belong to separate islands, and hence that they cannot touch. This means that we can fill in the cell between them as black.
2) Filled cells cannot be isolated in nurikabe
Remember that the filled cells must make up a continuous area; therefore none can be isolated.
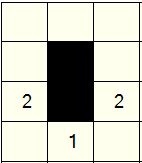
In the position we have reached with the section of puzzle above, we have filled in the cell between the two '2's.
However, that filled cell must be connected to all the other filled cells in the puzzle. Since the cells to its left, right and below already contain a number, it can only be connected through the cell above. Therefore this cell can be filled in this nurikabe puzzle.
Therefore in this sub-section of a puzzle we can instantly fill in these two cells:
3) Fill in cells that no island can reach
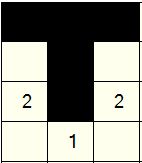
If a cell in the puzzle cannot be reached by any island, then you know it must be filled and can fill it in.
If we imagine the section of puzzle above for instance was a discrete puzzle on its own, then we can see that the top right, top middle and top left cells cannot be reached by either of the islands containing two cells. Therefore we can mark these as filled, like this:
4) Use potential 2 x 2 filled cells to solve nurikabe
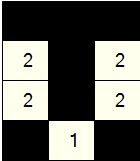
Often with a puzzle it will appear as though an island could be completed by moving in more than one direction. However the way it moves is often determined by applying the rule that no 2 x 2 block of filled cells may exist.
Look again at our sample puzzle, and imagine that the '1' were not there. We now don't know whether the '2' at the left side of the puzzle moves up or down to complete this island.
However, if it were to move downwards, there would be a 2 x 2 of filled cells appear as the cell above the 2 would be filled.
Since this isn't allowed, we know that the cell above the 2 must complete that island.
Therefore we can finish this section of the puzzle.
 ©
©