
|




Instructions
An Isolate puzzle will look like the one below but sometimes the grid will be a different size and contain a different number of square dots and inner walls:
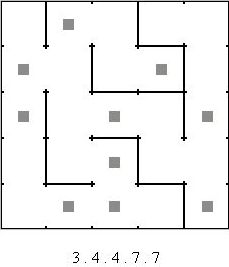
Each puzzle is composed of a grid containing + signs that can be connected to each other by walls; some walls may already be drawn in. Separate to the grid are a set of numbers which represent the area sizes present in the completed puzzle.
To solve the puzzle you must draw walls between + signs to create areas that contain the given number of squares. In the example above this means that the 25 squares in the grid need to be separated into areas of 3, 4, 4, 7 and 7 squares.
There are two key constraints; firstly each area must contain exactly two square dots and secondly each + sign must be connected to at least two walls.
Isolate Hints
Here are a few hints to help you solve the puzzles:
Cross out each area as it is found so that you only use it once.
Use pencil marks to keep track of which squares must belong to the same area.
Squares that have only one neighbour must link together because the puzzle has a minimum area size of 2 squares.
Areas cannot contain a 2x2 set of squares because that would leave a + sign linked to less than two walls. For example, the four squares in the top left of our example puzzle can not belong to the same area because the + sign is linked to only one wall.
Try to determine which square dots must appear together in the same area.
Remember all puzzles have one unique solution.
 ©
©