Non Consecutive Sudoku

Non consecutive sudoku is an interesting change to the standard puzzle, and introduces one key new rule. That rule is that, quite simply, the values placed in cells must be non-consecutive.

For instance, if one cell contains a '3' then the adjacent cells must not contain 2 or 4. We already know they cannot contain 3 because adjacent cells share at least one region with this number, and so under normal sudoku rules this means that they cannot contain the same number.

When solving non consecutive sudoku, this leads to some interesting rules. As well as the obvious one, that if a cell contains a placed number that you can knock out +/- 1 from adjacent cells, you can also work more subtle logic in.

For instance, let's say a cell contains either 3 or 4. Then we know that the adjacent cell cannot itself be 3 or 4, so we can remove those candidates from the cell. Why is this? Well, if the cell contains 3, then the banned numbers are 2 and 4 (and the adjacent cell can't be 3 as we've placed it here). If the cell contains 4, then the banned numbers are 3 and 5 (and the adjacent cell can't be 4 as we've placed it here). So, if we place 3, then 34 are banned, and if we place 4, then 34 are banned from the adjacent cell.

Other interesting pieces of logic also reveal themselves. There are a couple of types of non-consecutive sudoku. One uses markers between cells to show the cells that are non-consecutive in value. The other version has all cells in the grid as non consecutive, and that is the case with this puzzle. In fact, we've taken it even further - the non-consecutive nature even wraps around the edges of the puzzle - that is, the first and last cells in each row and column are also non-consecutive with each other! Print it off and see how you get on:
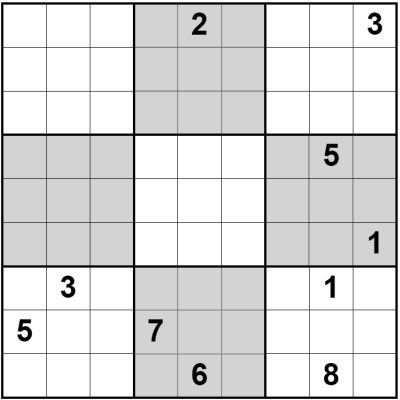